SVMの理解

目的

この章では
  • SVMの直観的な理解を得ます．

理論

線型分離可能なデータ

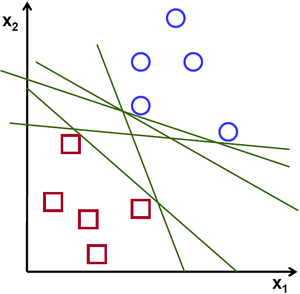
青と赤の2種類のデータを含む以下の画像を考えてみてください．k近傍法では，一つのテストデータに対して全ての学習データとの距離を測り，距離が最小となる学習データを検索結果としている．このような全探索は長い時間がかかり，メモリ使用量も増加してしまいます．画像中で与えられるデータを考慮すると，そこまでする必要があるのでしょうか？

Test Data

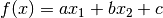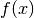他の方法を考えてみましょう．データを二つの領域に分割するような直線, f(x)=ax_1+bx_2+c を見つけます．新しいテストデータ X が得られた時，先ほど見つけた直線 f(x) を使って変換します．もし 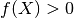f(X) > 0 であれば X は青のグループに属することになり，そうでなければ赤のグループに属することになります．この直線を 決定境界(Decision Boundary) と呼びます．この方法はとても簡潔でメモリ効率がよい方法です．一つの直線(高次元であれば超平面)によって二つのグループに分割可能なデータを 線型分離可能(Linear Separable) と言います．

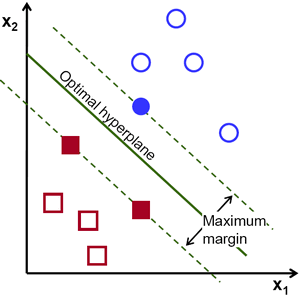
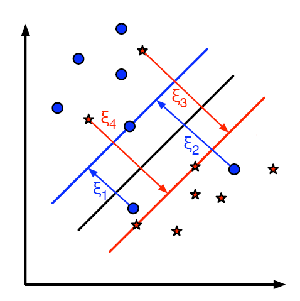
上記の画像であればそのような直線が大量に存在することが分かりますが，どの直線を選べば良いでしょうか?直感的には，全ての点からできるだけ遠くを通るような直線を選ぶべきだと言えますが，その理由は何故でしょうか?なぜなら，入力されるデータにはノイズが含まれる可能性があるからです．ノイズが含まれるデータに対して分類の精度が影響されないようにするべきです．そのため，データ点から最も遠い直線を選ぶとノイズに対するロバスト性が向上することになります．つまり，SVMが行うのは学習データに対する最小の距離を最大化するような直線(超平面)を見つけるということになります．以下の図の中心を通る太い線をみてください．

Decision Boundary

この決定境界を見つけるためには学習データが必要です．あらゆるデータが必要かと言うとそうではありません．自分と違うグループに近いデータがあれば十分です．例として示した画像では，青く塗りつぶされた円と赤く塗りつぶされた四角があれば十分です．これらのデータを サポートベクター(Support Vectors) と呼び，サポートベクターの間を通る直線を サポートプレーン(Support Planes) と呼ぶ． サポートベクターは決定境界の計算に適しており，全データを保持する必要がないためデータ削減において役に立つ．

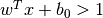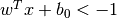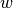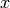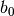まず初めにデータを最も良く表現する二つの超平面を見つけます．上の図で言うと，青のデータは w^Tx+b_0 > 1 という超平面によって表され，赤のデータは w^Tx+b_0 < -1 という超平面で表されます．ここで， w は 重みベクター(weight vector) ( w=[w_1, w_2,..., w_n])， x は特徴ベクター (x = [x_1,x_2,..., x_n])， b_0 は バイアス(bias) を表します．重みベクターは決定境界の傾きを表し，バイアスは決定境界の位置を表すパラメータです．

決定境界はこの二つの超平面の間に定義されます．すなわち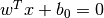， w^Tx+b_0 = 0 と表現できます．サポートベクターから決定境界までの最短距離は 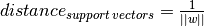distance_{support \, vectors}=\frac{1}{||w||} となります．マージンはこの距離の二倍になり，このマージンを最大化する必要があります．つまり，新しい関数
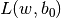L(w, b_0) を，幾つかの制約条件のもと最小化する必要があり，以下のように定式化出来ます:

\min_{w, b_0} L(w, b_0) = \frac{1}{2}||w||^2 \; \text{subject to} \; t_i(w^Tx+b_0) \geq 1 \; \forall i

ここで t_i \in [-1,1] は各クラスのラベルを意味します．

非線形分離可能データ

一つの直線では文理不可能なデータを考えます．例えば，’X’ が-3と+3，’O’が -1と+1という値を取る1次元のデータを考えます．このデータは明らかに線型文理不可能です．しかし，このようなデータを識別する方法gああります．もしこのデータセットをある関数 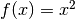f(x) = x^2, で写像すると，’X’ は 9，’O’ は1となるため線型分離可能となります．

そうでなければ，これらのデータを1次元から2次元へと変換します．関数 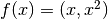f(x)=(x,x^2) を使って写像すると， ‘X’ は(-3,9)と(3,9)となり，’O’は(-1,1)と(1,1)となります．この写像後のデータも線型分離可能です．要するに，低次元空間で非線形分離可能なデータを高次元空間で線型分離可能と変換すると可能性が増えるわけです．

一般的には，線型分離性の可能性を確認するために，あるd次元空間のデータを別のD次元空間 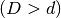(D>d) のデータに写像することが可能です．高次元(カーネル)空間における内積(dot product)計算を低次元入力(特徴)空間での処理によって計算するよう助けるアイディアがあります．以下の図を例に説明します．

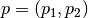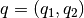2次元空間中の2点 p=(p_1,p_2) と q=(q_1,q_2) を考えます．以下の式に示すように2次元点を3次元空間へ写像する関数を 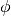\phi とします:

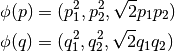
\phi (p) &= (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2) \\ \phi (q) &= (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2)

2点の内積を計算するカーネル関数 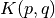K(p,q) を以下のように定義します:

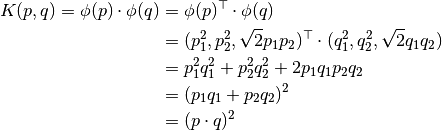
K(p,q) = \phi(p) \cdot \phi(q) &= \phi(p)^\top \cdot \phi(q) \\ &= (p_{1}^2,p_{2}^2,\sqrt{2} p_1 p_2)^\top \cdot (q_{1}^2,q_{2}^2,\sqrt{2} q_1 q_2) \\ &= p_{1}^2 q_{1}^2 + p_{2}^2 q_{2}^2 + 2 p_1 q_1 p_2 q_2 \\ &= (p_1 q_1 + p_2 q_2)^2 \\ &= (p \cdot q)^2

これは，3次元空間における内積が2次元空間での内積の2乗によって計算できることを意味します．この計算方法は，より高次元な空間でも適用可能です．つまり，高次元な特徴ベクターの内積計算を低次元空間における計算によって行えるわけです．一度特徴ベクターを写像してしまえば，高次元空間が取得できることになります．

これらの概念に加え，誤分類の問題があります．ただ単にマージンを最大化する決定境界だけでは十分ではなく，誤分類によるエラーの問題も考慮しなければいけません．マージンが最大ではなくても誤分類を減らせる決定境界が存在するかもしれません．とにかく，私たちは最大マージンであると共に誤分類が少なくなるような決定領域を見つけられるようにモデルを変更する必要があります．最小化の尺度は以下のように変更されます:

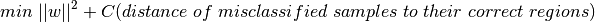
min \; ||w||^2 + C(distance \; of \; misclassified \; samples \; to \; their \; correct \; regions)

下図はこの概念を示しています．学習データ中の各サンプル点に対して新しいパラメータ 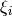\xi_i を定義します．このパラメータは対応する学習サンプルからその正しい決定領域への距離を表しています．誤分類されていないサンプル点は対応するサポートプレーンに向かっていくため距離はゼロとなります．

It is the distance from its corresponding training sample to their correct decision region. For those who are not misclassified, they fall on their corresponding support planes, so their distance is zero.

Misclassification

新しい最適化問題は以下のようになります:

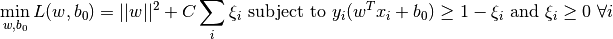
\min_{w, b_{0}} L(w,b_0) = ||w||^{2} + C \sum_{i} {\xi_{i}} \text{ subject to } y_{i}(w^{T} x_{i} + b_{0}) \geq 1 - \xi_{i} \text{ and } \xi_{i} \geq 0 \text{ } \forall i

式中のパラメータCをどのように選ぶべきでしょうか?その答えは学習データがどのように分布しているのかに依存しています．一般的な答えは存在しませんが，以下のルールを考慮すると役立つでしょう:

  • Cの値を大きくすると誤分類エラーを少なくできるがマージンが小さくなってしまう．この時誤分類エラーを起こすとエネルギーが大きくなります．最適化は変数の最小化を目的とするため，少ない誤分類のエラーしか許容されません．
  • Cの値を小さくするとマージンが大きくなる一方で誤分類のエラーが増えます．この時最小化は総和の項を重視しないため，マージンが大きい超平面の発見に重きを置くことになります．

課題