画像のしきい値処理¶
目的¶
- このチュートリアルでは大局的しきい値処理,適応的しきい値処理,大津の二値化などを学びます.
- 以下の関数の使い方を学びます : cv2.threshold, cv2.adaptiveThreshold etc.
単純なしきい値処理¶
方法は単純です.あるがその画素値がしきい値より大きければある値(白)を割り当て,そうでなければ別の値(黒)を割り当てます.関数は cv2.threshold を使います.第1引数は入力画像で グレースケール画像でなければいけません .第2引数はしきい値で,画素値を識別するために使われます.第3引数は最大値でしきい値以上(指定するフラグ次第では以下)の値を持つ画素に対して割り当てられる値です.OpenCVは幾つかのしきい値処理を用意しており,第4引数にて指定します.以下がフラグの一覧です:
- cv2.THRESH_BINARY
- cv2.THRESH_BINARY_INV
- cv2.THRESH_TRUNC
- cv2.THRESH_TOZERO
- cv2.THRESH_TOZERO_INV
OpenCVの公式ドキュメントに各フラグがどのよな処理をするか記載されているので,確認してください.
cv2.threshold は二つの出力を返します.一つ目の出力 retval については後述します.二つ目の出力がしきい値処理された後の 二値画像 になります.
コード :
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('gradient.png',0)
ret,thresh1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
ret,thresh2 = cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV)
ret,thresh3 = cv2.threshold(img,127,255,cv2.THRESH_TRUNC)
ret,thresh4 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO)
ret,thresh5 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV)
titles = ['Original Image','BINARY','BINARY_INV','TRUNC','TOZERO','TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
for i in xrange(6):
plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
Note
複数の画像をまとめて表示するためにmatplotlibの plt.subplot() 関数を使っています.詳細についてはmatplotlibのドキュメントを参照してください..
以下が結果画像の一覧です :
適応的しきい値処理¶
前の例ではある画像に対して一つのしきい値を与えてしきい値処理をしましたが,撮影状況などによって画像上の領域ごとに異なる光源環境になってしまっているような画像に対して期待するような結果が得られません.そのような状況では適応的しきい値処理を使うと良いでしょう.適応的しきい値処理では,画像中の小領域ごとにしきい値の値を計算します.そのため領域ごとに光源環境が変わってしまうような画像に対して,単純なしきい値処理より良い結果が得られます.
適応的しきい値処理には cv2.adaptiveThreshold 関数を使用し,以下に示す3つの ‘特殊な’ 入力パラメータ指定します.cv2.threshold とは異なり,出力は一つ(二値画像)しかありません.
- しきい値の計算方法 - 小領域中でのしきい値の計算方法.
- cv2.ADAPTIVE_THRESH_MEAN_C : 近傍領域の中央値をしきい値とします.
- cv2.ADAPTIVE_THRESH_GAUSSIAN_C : 近傍領域の重み付け平均値をしきい値とします.重みの値はGaussian分布になるように計算されます.
Block Size - しきい値計算に使用する近傍領域のサイズ.1より大きい奇数を指定する必要があります.
C - 計算されたしきい値から引く定数です.
以下に,領域ごとに光源環境が大きく異なる画像に対して,単純なしきい値処理と適応的しきい値処理でどのように異なる結果が得られるかを示します:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('dave.jpg',0)
img = cv2.medianBlur(img,5)
ret,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
th2 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_MEAN_C,\
cv2.THRESH_BINARY,11,2)
th3 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,\
cv2.THRESH_BINARY,11,2)
titles = ['Original Image', 'Global Thresholding (v = 127)',
'Adaptive Mean Thresholding', 'Adaptive Gaussian Thresholding']
images = [img, th1, th2, th3]
for i in xrange(4):
plt.subplot(2,2,i+1),plt.imshow(images[i],'gray')
plt.title(titles[i])
plt.xticks([]),plt.yticks([])
plt.show()
結果 :
大津の二値化¶
前述しましたが,cv2.threshold 関数の二つ目の出力 retVal は大津の二値化に使われます.
大局的しきい値処理ではしきい値の値は任意に定めることができます.では,どのような値を選べば良いのでしょうか?トライアンドエラーを繰り返せばいいわけですが,ここでは入力画像が bimodal image (ヒストグラムが双峰性を持つような画像)であることを仮定します.(そのような画像に対して,二つのピークの間の値をしきい値として選べば良いような気がしませんか?これが大津の二値化が行っている処理です.簡単に説明すると,画像のヒストグラムを基にしきい値を決定する方法と言えます.そのため,双峰生を持たないヒストグラムを持つ画像に対しては良い結果が得られないでしょう.
関数は大局的しきい値処理と同じ cv2.threshold を使いますが,フラグに cv2.THRESH_OTSU も一緒に追加する必要が有ります.. しきい値は0を指定しましょう.アルゴリズムが自動的にしきい値を計算し てくれ,二つ目の出力値である retVal として返してくれます.大津の二値化を使わない場合, retVal の値は入力引数に指定したしきい値と同じ値になります.
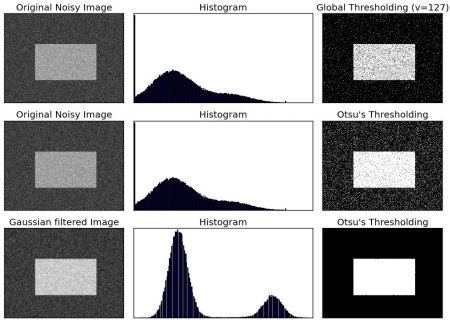
以下の例を見てください.ノイズが含まれる入力画像に対して異なる3つの方法を試しています.一つ目の方法はしきい値を127に設定した単純なしきい値処理です.二つ目の方法は大津の二値化を適用します.三つ目の方法は,5x5のサイズのgaussianフィルタでノイズを抑制した画像に対して大津の二値化を適用します. 平滑化処理によってノイズの影響が軽減されていることが分かります.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('noisy2.png',0)
# global thresholding
ret1,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
# Otsu's thresholding
ret2,th2 = cv2.threshold(img,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
# Otsu's thresholding after Gaussian filtering
blur = cv2.GaussianBlur(img,(5,5),0)
ret3,th3 = cv2.threshold(blur,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
# plot all the images and their histograms
images = [img, 0, th1,
img, 0, th2,
blur, 0, th3]
titles = ['Original Noisy Image','Histogram','Global Thresholding (v=127)',
'Original Noisy Image','Histogram',"Otsu's Thresholding",
'Gaussian filtered Image','Histogram',"Otsu's Thresholding"]
for i in xrange(3):
plt.subplot(3,3,i*3+1),plt.imshow(images[i*3],'gray')
plt.title(titles[i*3]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+2),plt.hist(images[i*3].ravel(),256)
plt.title(titles[i*3+1]), plt.xticks([]), plt.yticks([])
plt.subplot(3,3,i*3+3),plt.imshow(images[i*3+2],'gray')
plt.title(titles[i*3+2]), plt.xticks([]), plt.yticks([])
plt.show()
結果 :
大津の二値化の仕組み¶
ここでは大津の二値化のPythonでの実装方法を説明します.興味がない人は飛ばして構いません.
双峰生ヒストグラムを持つ画像を扱っているので,大津のアルゴリズムは以下の式によって定義される 重み付けされたクラス内分散 を最小にするようなしきい値 (t) を探します :
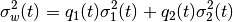
ここで各変数は以下のように定義されます.
![q_1(t) = \sum_{i=1}^{t} P(i) \quad \& \quad q_1(t) = \sum_{i=t+1}^{I} P(i)
\mu_1(t) = \sum_{i=1}^{t} \frac{iP(i)}{q_1(t)} \quad \& \quad \mu_2(t) = \sum_{i=t+1}^{I} \frac{iP(i)}{q_2(t)}
\sigma_1^2(t) = \sum_{i=1}^{t} [i-\mu_1(t)]^2 \frac{P(i)}{q_1(t)} \quad \& \quad \sigma_2^2(t) = \sum_{i=t+1}^{I} [i-\mu_1(t)]^2 \frac{P(i)}{q_2(t)}](../../../_images/math/588a446d9a466ac81104cf588afec8ec9d713ffe.png)
具体的には,双峰性ヒストグラムのピークの間に存在するしきい値,すなわち二値化によって分類される二つのクラスのクラス内分散を最小にするようなしきい値 t を計算しています.Pythonでの実装は以下のようになります:
img = cv2.imread('noisy2.png',0)
blur = cv2.GaussianBlur(img,(5,5),0)
# find normalized_histogram, and its cumulative distribution function
hist = cv2.calcHist([blur],[0],None,[256],[0,256])
hist_norm = hist.ravel()/hist.max()
Q = hist_norm.cumsum()
bins = np.arange(256)
fn_min = np.inf
thresh = -1
for i in xrange(1,256):
p1,p2 = np.hsplit(hist_norm,[i]) # probabilities
q1,q2 = Q[i],Q[255]-Q[i] # cum sum of classes
b1,b2 = np.hsplit(bins,[i]) # weights
# finding means and variances
m1,m2 = np.sum(p1*b1)/q1, np.sum(p2*b2)/q2
v1,v2 = np.sum(((b1-m1)**2)*p1)/q1,np.sum(((b2-m2)**2)*p2)/q2
# calculates the minimization function
fn = v1*q1 + v2*q2
if fn < fn_min:
fn_min = fn
thresh = i
# find otsu's threshold value with OpenCV function
ret, otsu = cv2.threshold(blur,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
print thresh,ret
(今までのチュートリアルで扱っていない関数を幾つか使用していますが,これ以降のチュートリアルで扱うので安心してください)
補足資料¶
- Digital Image Processing, Rafael C. Gonzalez
課題¶
- 大津の二値化のために使用可能な最適化方法が幾つか存在します.調べて実装してみてください.